You are here: Home >> Mathematics >> Area and Perimeter Formula
Formulas to find Area of Rectangle, Square, Parallelogram, Triangle, Circle, etc.
TIPS FOR SOLVING QUESTIONS RELATED TO AREA:
|
1. Square: A square is a plane figure with four equal straight sides and four right angles. Area of Square = (side)2 = (diagonal)2 divided by 2 Perimeter of Square = 4 x side 2. Rectangle: A rectangle is a four-sided shape that is made up of two pairs of parallel lines and that has
four right angles. Area of Rectangle = Length x Breadth Perimeter of Rectangle = 2(Length + Breadth) 3. Area of 4 walls of a room = 2(Length + Breadth) x Height |
4. Triangle: A triangle is a a plane figure with three straight sides and three angles.
(i) Right triangle with base and height given.
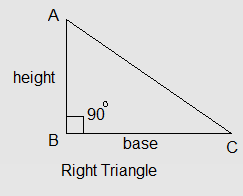
\begin{aligned} \text{Area of a triangle =} \frac{1}{2}*Base*Height \\
\end{aligned}
(ii) Triangle with three different sides a, b and c.
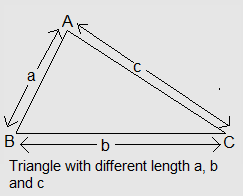
\begin{aligned} \text{Area of a triangle =}\sqrt{s(s-a)(s-b)(s-c)}, \\
\end{aligned}
\begin{aligned}
s= \frac{1}{2}(a+b+c) \\
\end{aligned}
(iii) Equilateral triangle - A triangle with all three sides of equal length.
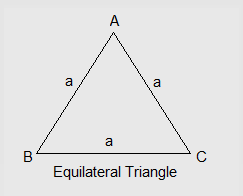
\begin{aligned} \text{Area of a equilateral triangle =}
\frac{\sqrt{3}}{4}*(side)^2
\end{aligned}
|
(iv). Radius of incircle of an equilateral triangle of side a = \begin{aligned} 5. Parallelogram: A parallelogram is a 4-sided flat shape with straight sides where opposite sides are parallel. |
6. Circle: A circle is a round plane figure whose boundary (the circumference) consists of points equidistant
from a fixed point (the centre).
(i) \begin{aligned} \text{Area of a circle} = \pi R^2 \end{aligned}, where R is radius of the circle
(ii) \begin{aligned} \text{Circumference of a circle} = 2 \pi R \end{aligned}
(iii) \begin{aligned} \text{Length of a arc} = \frac{2 \pi R \theta }{360} \\
\text{ where } \theta \text{ is the central angle } \end{aligned}
(iv)
\begin{aligned} \text{Area of sector = } \frac{1}{2}(arc* \theta) \\
= \frac{\pi R^2 \theta}{360}
\end{aligned}
(v)
\begin{aligned} \text{Area of a semi circle =} \frac{\pi R^2}{2} \end{aligned}
(vi)
\begin{aligned}\text{Circumference of a semi circle =} \pi R \end{aligned}

